Skip to contents

Gravity model

Source: vignettes/gravity_model.Rmd
gravity_model.Rmd
## OpenMP detected, parallel computations will be performed.
## 
## Attaching package: 'cppSim'
## The following object is masked _by_ '.GlobalEnv':
## 
##     run_model

This file will cover the process of building a local version of the gravity model used to predict cycling and/or walking flows across London.

What model to use ?

The general version of the doubly constrained gravity model looks the following way: Tij=AiBjOiDjf(cij) T_{ij} = A_iB_jO_iD_jf(c_{ij}) where OiO_i is the working population of the origin, and DjD_j is the available workplaces at the destination location: Oi=∑jTij O_i = \sum_j T_{ij} Dj=∑iTij D_j = \sum_i T_{ij}

The terms AiA_i,BjB_j are factors for each location. The derivation of these factors is based on the relation:

Ai=[∑jBjDjf(cij)]−1A_i = [\sum_j B_jD_jf(c_{ij})]^{-1}

Bj=[∑iAiOif(cij)]−1B_j = [\sum_i A_iO_if(c_{ij})]^{-1}

with the derivation made from a recursive chain with initial values 1. Let’s refer to the parameters above as vectors A→\vec{A},B→\vec{B},O→\vec{O},D→\vec{D}, and to the cost function and flow as matrices F and T such that Fij=f(cij)F_{ij}=f(c_{ij}) and TijT_{ij} is a flow from i to j.

# creating the O, D vectors. 
O <- apply(flows_test, sum, MARGIN = 2) |> c()

D <- apply(flows_test, sum, MARGIN = 1) |> c()
F_c <- cost_function(distance_test,1,type = "exp")

Next, we need to run the recursive procedure until the values stabilise. We introduce the threshold at which we will stop running the recursion δ\delta. It corresponds to the rate of change of the parameter with respect to the previous iteration.

beta_calib <- foreach::foreach(i = 28:33
                               ,.combine = rbind) %do% {
                                 beta <- 0.1*(i - 1)
                                 print(paste0("RUNNING MODEL FOR beta = ",beta))
                                 run <- run_model(flows = flows_test
                                                  ,distance = distance_test
                                                  ,beta = beta
                                                  ,type = "exp"
                                 )
                             
                                 cbind(beta, run$r2,run$rmse)
                               }
## [1] "RUNNING MODEL FOR beta = 2.7"
## [1] "cost function computed"
## [1] "calibration: over"
## [1] "model run: over"
## [1] "E_sor = 0.392146371104884"
## [1] "r2 = 0.314777655460119"
## [1] "RMSE = 22163551"
## [1] "RUNNING MODEL FOR beta = 2.8"
## [1] "cost function computed"
## [1] "calibration: over"
## [1] "model run: over"
## [1] "E_sor = 0.39249333259527"
## [1] "r2 = 0.314658641698322"
## [1] "RMSE = 22135915"
## [1] "RUNNING MODEL FOR beta = 2.9"
## [1] "cost function computed"
## [1] "calibration: over"
## [1] "model run: over"
## [1] "E_sor = 0.39273122700898"
## [1] "r2 = 0.314581076323428"
## [1] "RMSE = 22112582"
## [1] "RUNNING MODEL FOR beta = 3"
## [1] "cost function computed"
## [1] "calibration: over"
## [1] "model run: over"
## [1] "E_sor = 0.392611773609201"
## [1] "r2 = 0.314218919524871"
## [1] "RMSE = 22102764"
## [1] "RUNNING MODEL FOR beta = 3.1"
## [1] "cost function computed"
## [1] "calibration: over"
## [1] "model run: over"
## [1] "E_sor = 0.392377057376276"
## [1] "r2 = 0.313849972411283"
## [1] "RMSE = 22098059"
## [1] "RUNNING MODEL FOR beta = 3.2"
## [1] "cost function computed"
## [1] "calibration: over"
## [1] "model run: over"
## [1] "E_sor = 0.391924520987228"
## [1] "r2 = 0.313306091157044"
## [1] "RMSE = 22103251"
plot(beta_calib[,1]
     ,beta_calib[,2]
     ,xlab = "beta value"
     ,ylab = "quality of fit, r"
     ,main = "influence of beta on the goodness of fit"
     ,pch = 19
     ,cex = 0.5
     ,type = "b")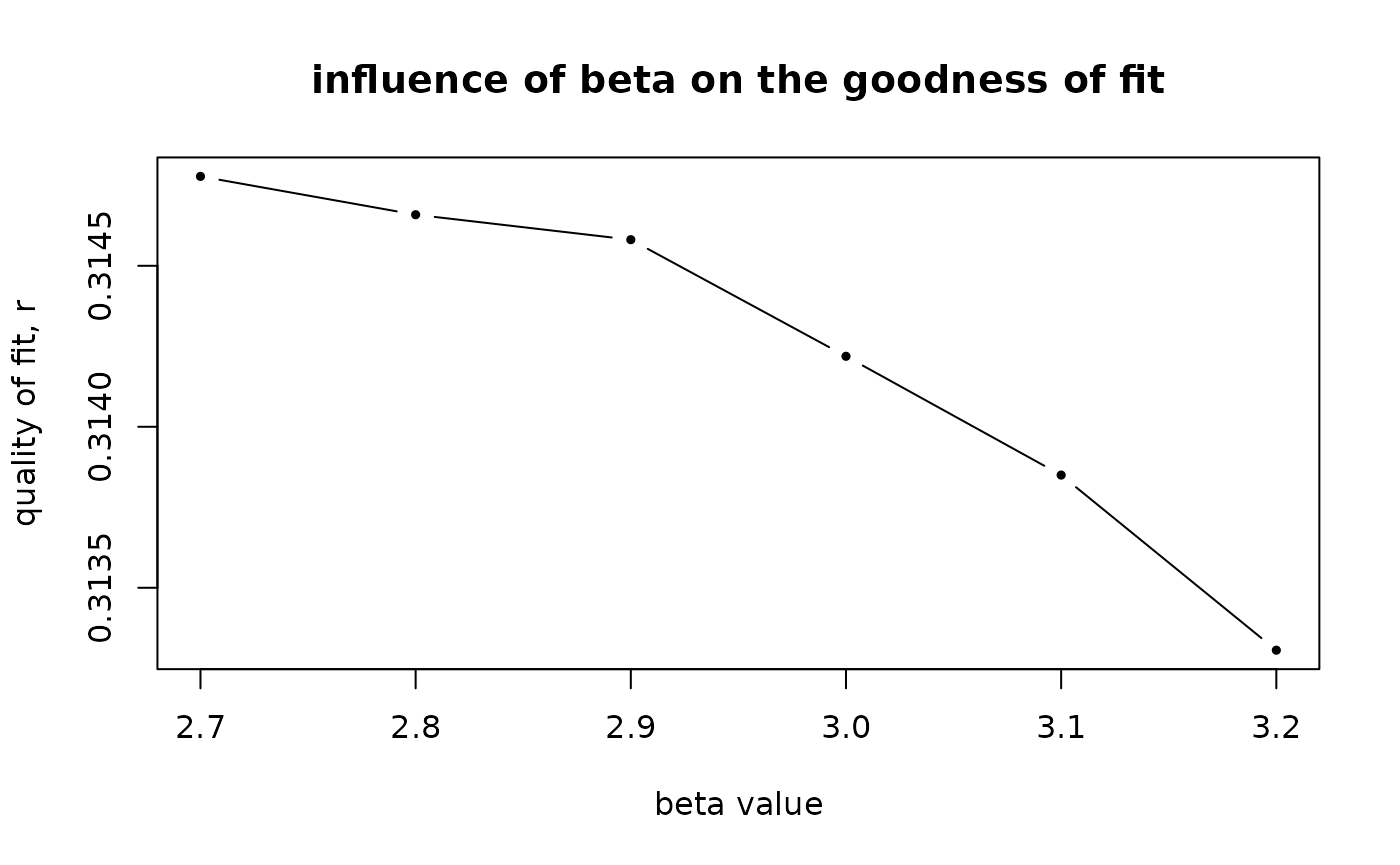

beta_best_fit <- beta_calib[which(beta_calib[,2] == max(beta_calib[,2])),1]
x <- seq_len(100)/20
plot(x
     ,exp(-beta_best_fit*x)
     ,main = "cost function"
     ,xlab = "distance, km"
     ,ylab = "decay factor"
     ,pch = 19
     ,cex = 0.5
     ,type = "l")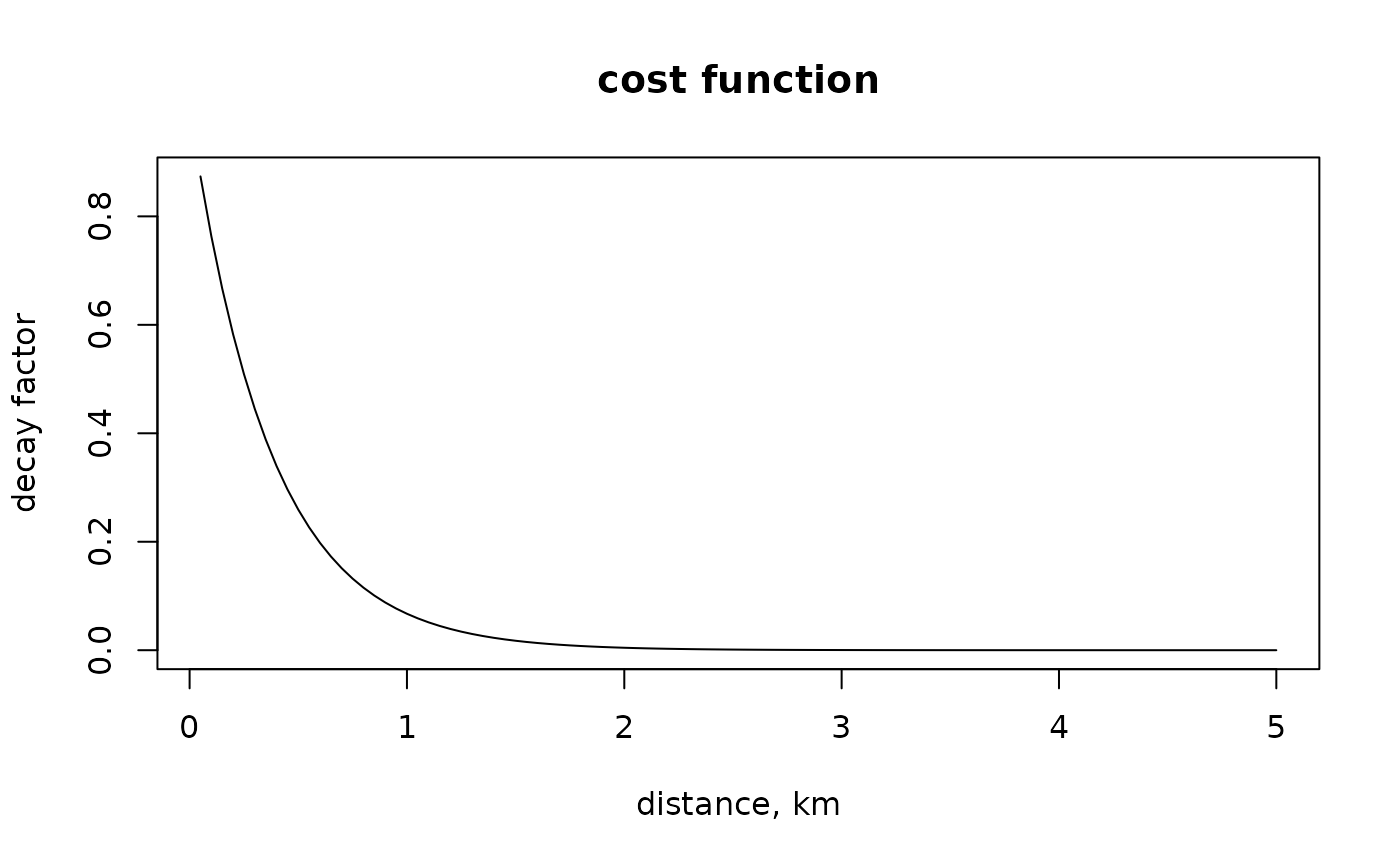

run_best_fit <- run_model(flows = flows_test
                 ,distance = distance_test
                 ,beta = beta_best_fit
                 ,type = "exp"
                 )
## [1] "cost function computed"
## [1] "calibration: over"
## [1] "model run: over"
## [1] "E_sor = 0.392146371104884"
## [1] "r2 = 0.314777655460119"
## [1] "RMSE = 22163551"
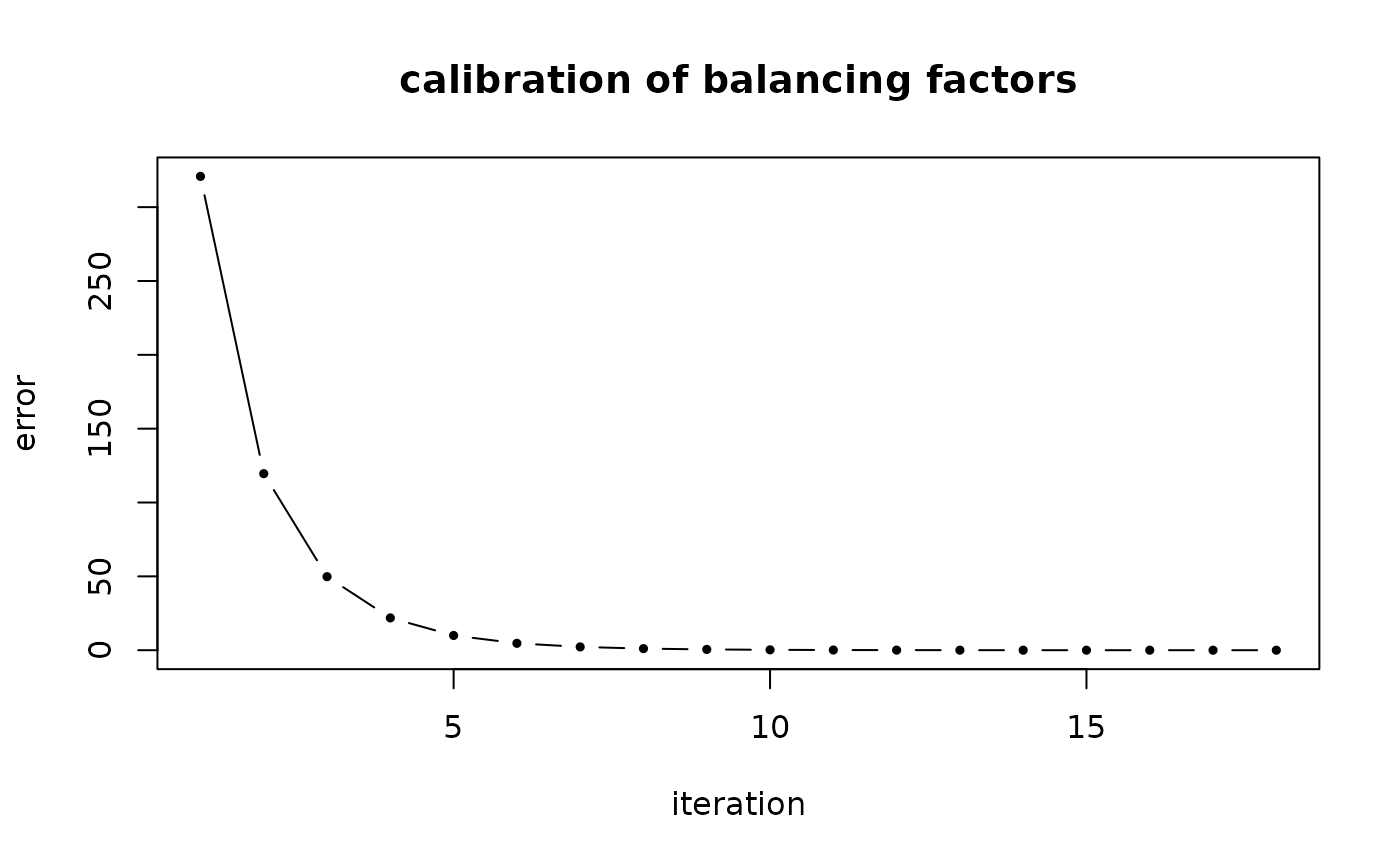
plot(seq_along(run_best_fit$calib)
     ,run_best_fit$calib
     ,xlab = "iteration"
     ,ylab = "error"
     ,main = "calibration of balancing factors"
     ,pch = 19
     ,cex = 0.5
     ,type = "b"
     
)

plot(flows_test
     ,run_best_fit$values
     ,ylab = "flows model"
     ,xlab = "flows"
     ,log = "xy"
     ,pch = 19
     ,cex = 0.5)
lines(seq_len(max(run_best_fit$values))
      ,seq_len(max(run_best_fit$values))
      ,col = "darkred"
      ,lwd = 2)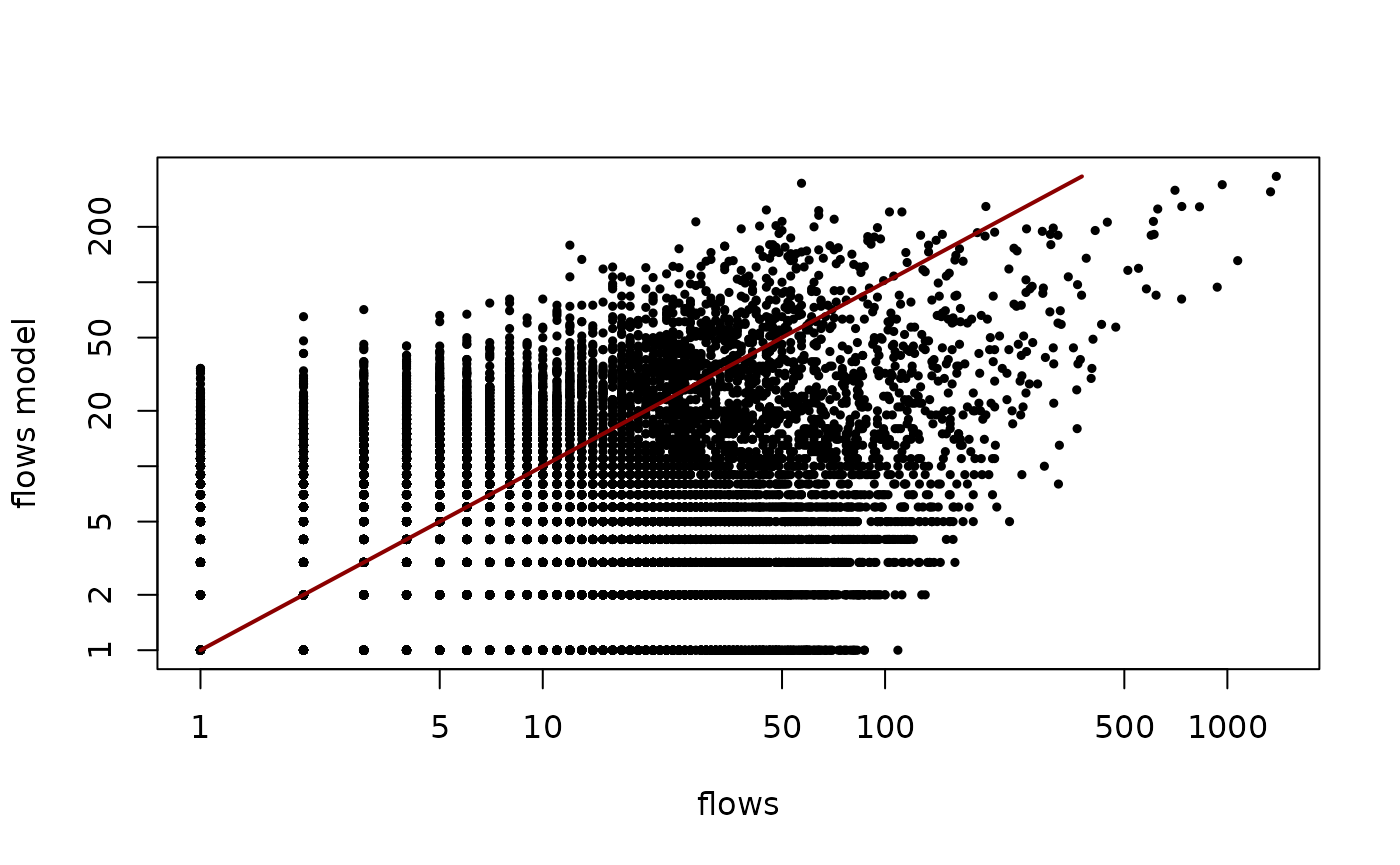

## MODEL USING THE GLM And POISSON DISTRIBUTION

# flows_london <- rlist::list.load("flows_london.rds")

data(flows_london)

flows_london <- flows_london

sample_od <- sample(unique(flows_london$workplace),100)

flows_grav <- flows_london[(workplace %in% sample_od) & (residence %in% sample_od),]

flows_grav[,O := sum(bike),by = from_id]

flows_grav[,D := sum(bike), by = to_id]

#

model <- glm(bike ~ workplace+residence+distance -1
             ,data = flows_grav
             ,family = poisson(link = "log")
             )

((model$fitted.values - flows_grav$bike)) |> hist(breaks = 100)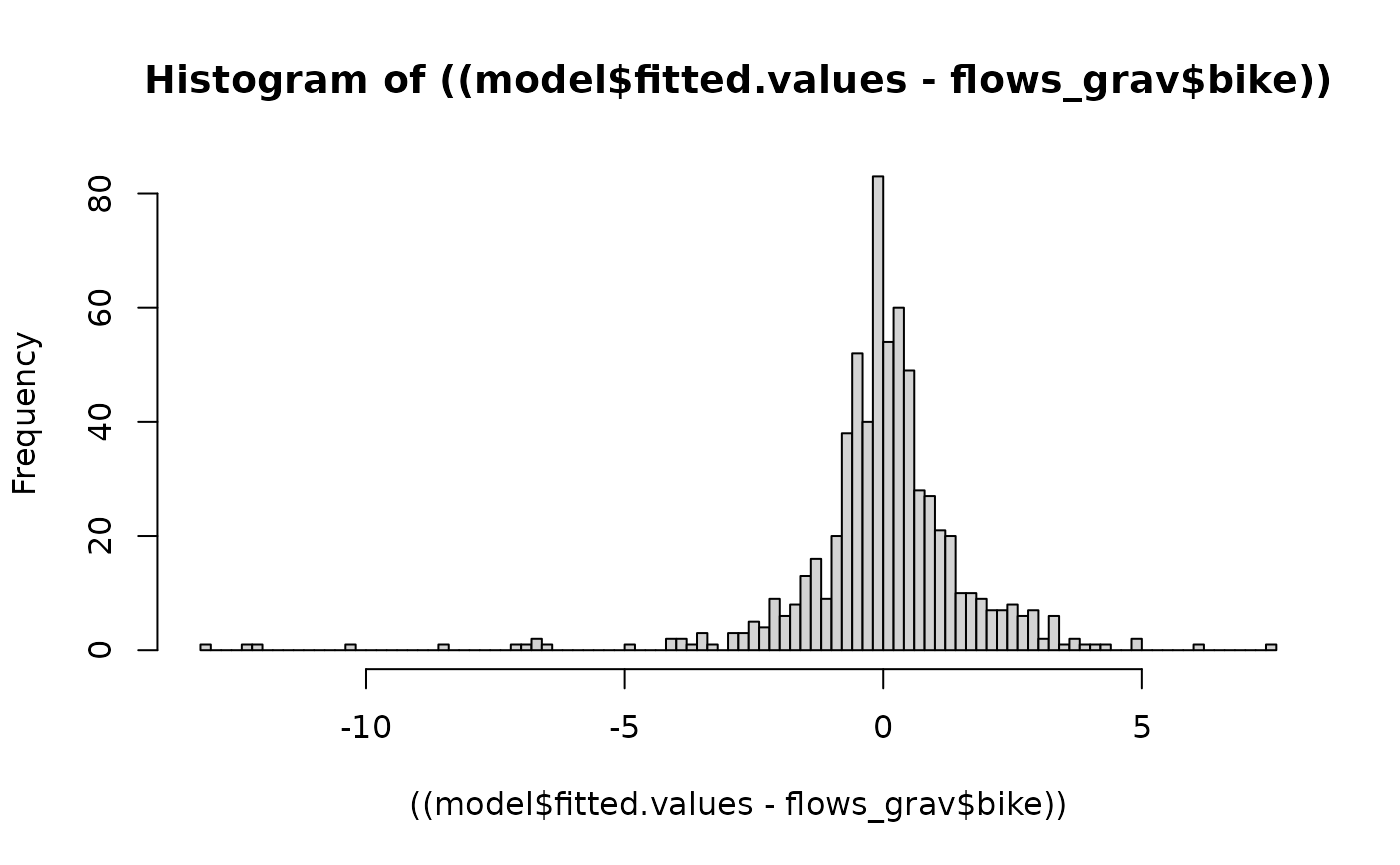

r2 <- r_2(flows_grav$bike,model$fitted.values)
r2
## [1] 0.8854178

Support functions 

print("cost function:")
## [1] "cost function:"
cost_function
## function (d, beta, type = "exp") 
## {
##     if (type == "exp") {
##         exp(-beta * d)
##     }
##     else if (type == "pow") {
##         d^(-beta)
##     }
##     else {
##         print("provide a type of functino to compute")
##     }
## }
## <bytecode: 0x55e1ac389570>
print("calibration function:")
## [1] "calibration function:"
calibration
## function (cost_fun, O, D, delta = 0.05) 
## {
##     B <- rep_len(1, nrow(cost_fun))
##     eps <- abs(sum(B))
##     e <- NULL
##     i <- 0
##     while ((eps > delta) & (i < 50)) {
##         A_new <- 1/(apply(cost_fun, function(x) sum(B * D * x), 
##             MARGIN = 1))
##         B_new <- 1/(apply(cost_fun, function(x) sum(A_new * O * 
##             x), MARGIN = 2))
##         eps <- abs(sum(B_new - B))
##         e <- append(e, eps)
##         A <- A_new
##         B <- B_new
##         i <- i + 1
##     }
##     list(A = A, B = B, e = e)
## }
## <bytecode: 0x55e1ab4f6ee8>
print("model run")
## [1] "model run"
run_model
## function (flows, distance, beta = 0.25, type = "exp") 
## {
##     F_c <- cost_function(d = {
##         {
##             distance
##         }
##     }, beta = {
##         {
##             beta
##         }
##     }, type = type)
##     print("cost function computed")
##     O <- as.integer(apply(flows, sum, MARGIN = 1))
##     D <- as.integer(apply(flows, sum, MARGIN = 2))
##     A_B <- calibration(cost_fun = F_c, O = O, D = D, delta = 0.001)
##     print("calibration: over")
##     A <- A_B$A
##     B <- A_B$B
##     flows_model <- foreach(j = c(1:nrow(F_c)), .combine = rbind) %do% 
##         {
##             round(A[j] * B * O[j] * D * F_c[j, ])
##         }
##     print("model run: over")
##     e_sor <- as.numeric(e_sorensen(flows, flows_model))
##     print(paste0("E_sor = ", e_sor))
##     r2 <- as.numeric(r_2(flows_model, flows))
##     print(paste0("r2 = ", r2))
##     RMSE <- as.numeric(rmse(flows_model, flows))
##     print(paste0("RMSE = ", RMSE))
##     list(values = flows_model, r2 = r2, rmse = RMSE, calib = A_B$e, 
##         e_sor = e_sor)
## }
## <bytecode: 0x55e1ac08e6e8>