Skip to contents

Getting started

Source: vignettes/getting_started_2.Rmd
getting_started_2.Rmd

Introduction

The cppSim package was developed in order to have the possibility to do spatial interaction models at scale on a regular spec machine. The few existing packages proposing similar functionality tend to prioritize the different functionalities, and end up being suited for small models, say a few dozen origins and destinations. But what if you want to analyse a whole city, region, or even country with potentially hundreds or thousands of ODs ? This is where cppSim steps in. This vignette will present a typical set up one might have when doing SIMs. And to keep it simple, we will focus only on the modelling part. This means we will cover the steps of getting data, building a network, routing in another, longer article. We will use the data sets that come with this package to demonstrate power of cppSim.

Set up

Let’s install and import the library and the data sets.

# remotes::install_github('ischlo/cppSim')

library(cppSim)

data("distance_test")
data("flows_test")
data("london_msoa")

The two data sets provided consist in the flow matrix flows_test with cycling and walking flows combined between every MSOA in Greater London. The data was obtained from the 2011 UK census open data portal. The second matrix is a distance matrix between the centroids of every MSOAs in Greater London. It was computed using the great cppRouting package and OpenStreetMap networks adapted to be suitable for cycling and walking. The networks can be downloaded in a good format with the python package OSMnx, or with the recently published, but yet under development cppRnet package in R

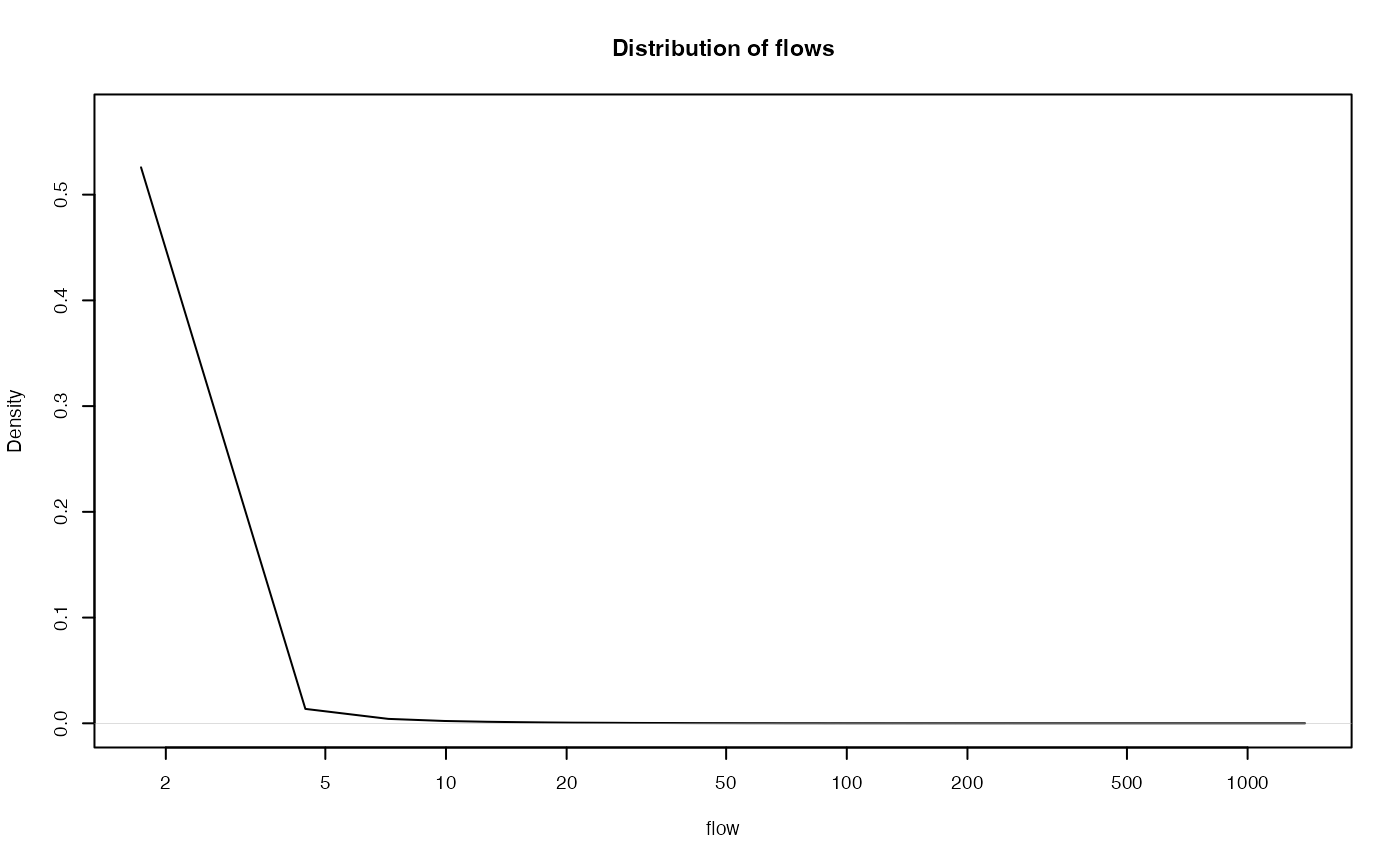
Let’s have a look at the size of these:


dim(distance_test)
#> [1] 983 983
dim(flows_test)
#> [1] 983 983
#> Warning in xy.coords(x, y, xlabel, ylabel, log): 1 x value <= 0 omitted from
#> logarithmic plot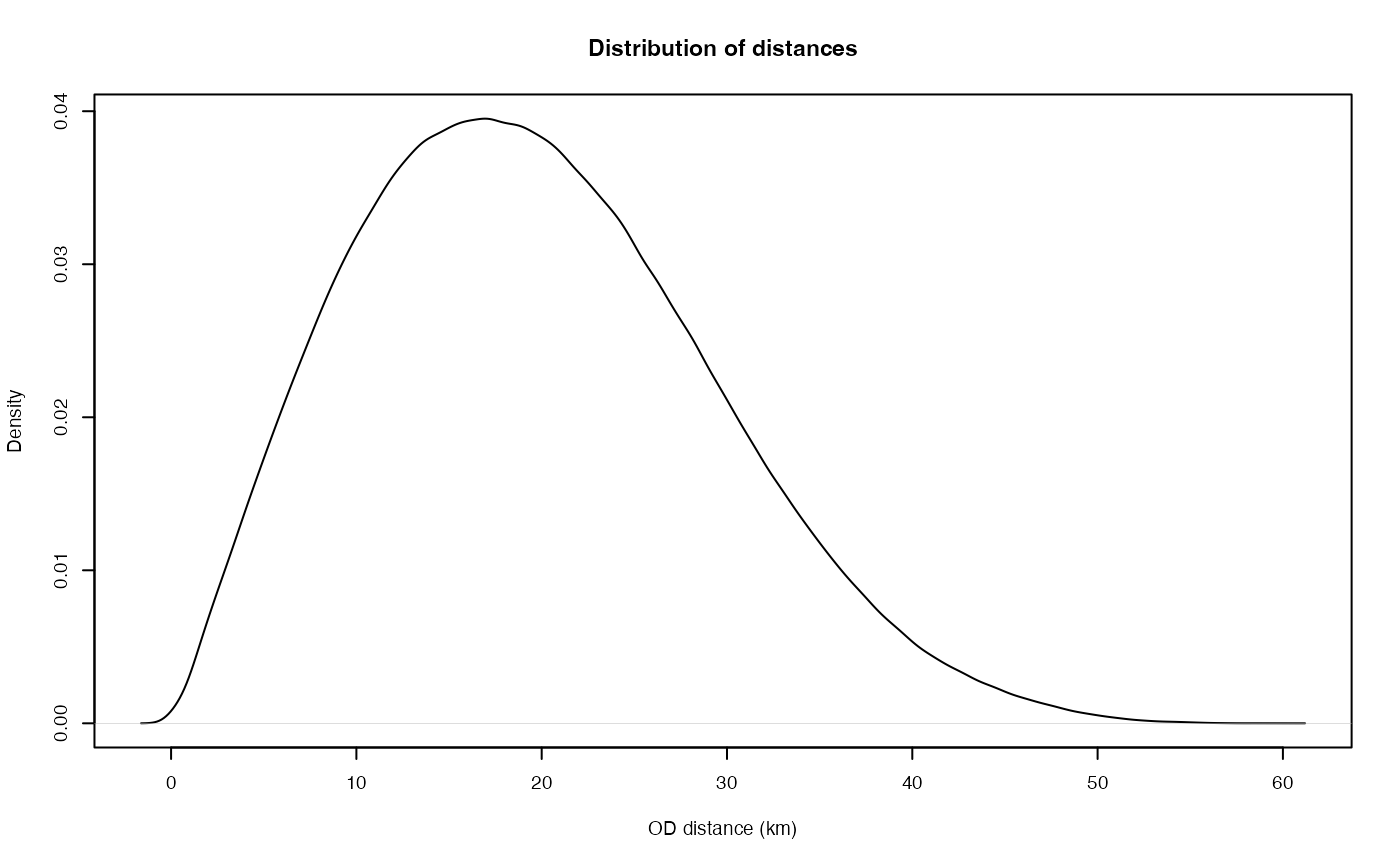

Visualisation

Model

If the coefficient of the distance decay (cost) function is known, one can simply run:


beta <- .1

res_model <- cppSim::run_model(flows = flows_test
                         ,distance = distance_test
                         ,beta = beta)

str(res_model)
#> List of 1
#>  $ values: num [1:983, 1:983] 283.6 5.6 14.3 10.8 12.7 ...

dim(res_model$values)
#> [1] 983 983

Let’s have a look at the correlation between the model output and data:

cor(c(res_model$values)
    ,c(flows_test))
#> [1] 0.5903494

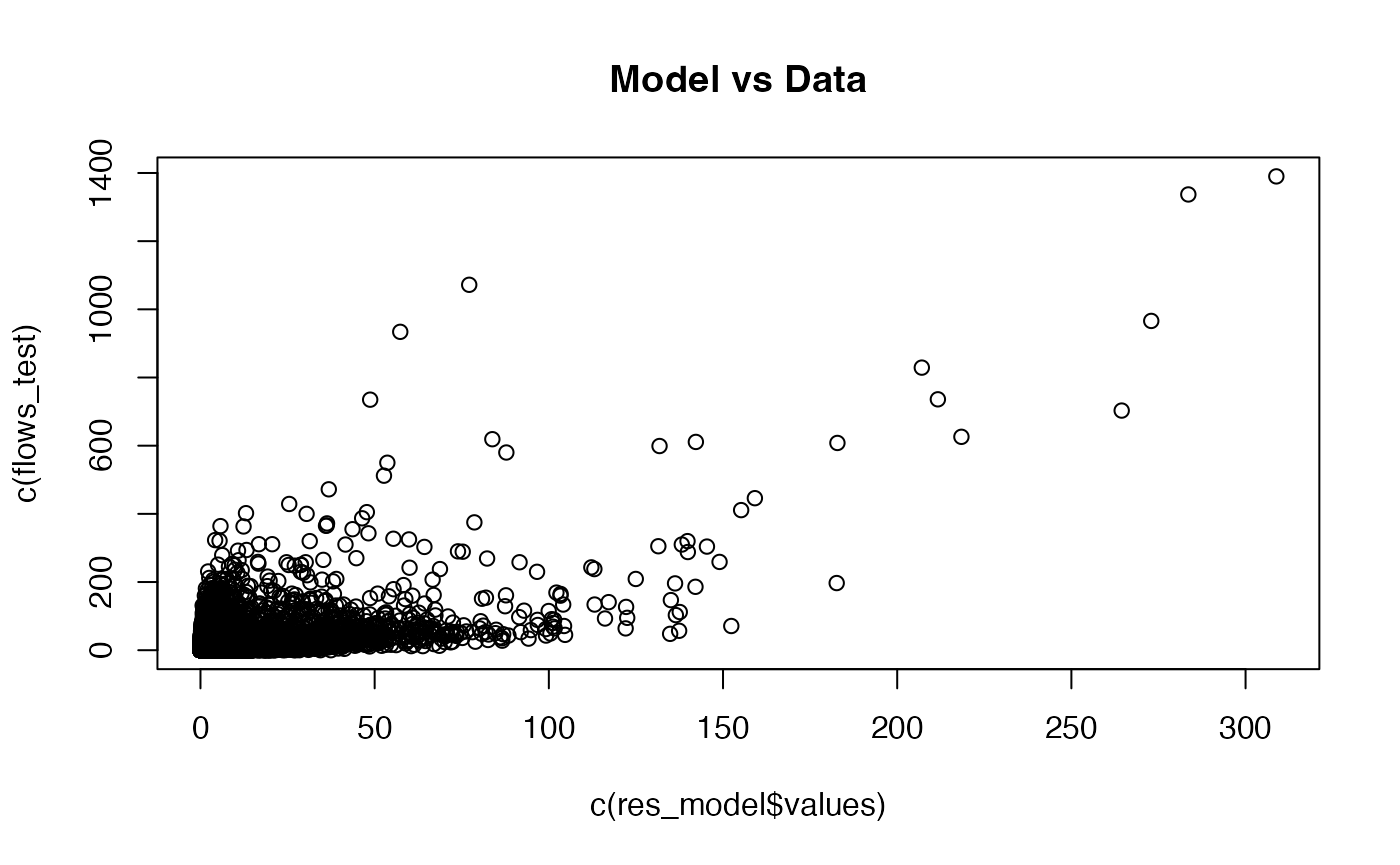
the correlation is already high, but we can do better, for that, we will need to calibrate the model. This is done with the simulation function, it will find the optimal cost function that gives the best fit.

Simulation

If you want to run a full simulation that will calibrate a model and determine the optimal distance decay coefficient, do the following:


res_sim <- cppSim::simulation(flows_matrix = flows_test
                          ,dist_matrix = distance_test
)

str(res_sim)
#> List of 2
#>  $ best_fit_values: num [1:983, 1:983] 1.43e+03 2.87e-03 9.48e-03 8.72e-04 8.05e-03 ...
#>  $ best_fit_beta  : num 0.962

res_sim$best_fit_beta
#> [1] 0.9615716

The output will be a list with two elements, first the output of a model run that best fits the observed data. Second, the optimal distance decay exponent that produces this result. This value will be relevant for further modelling. Let’s see some of the model results:

plot(res_sim$best_fit_values
     ,flows_test
     # ,log = 'xy'
     ,main = 'Model vs Data')

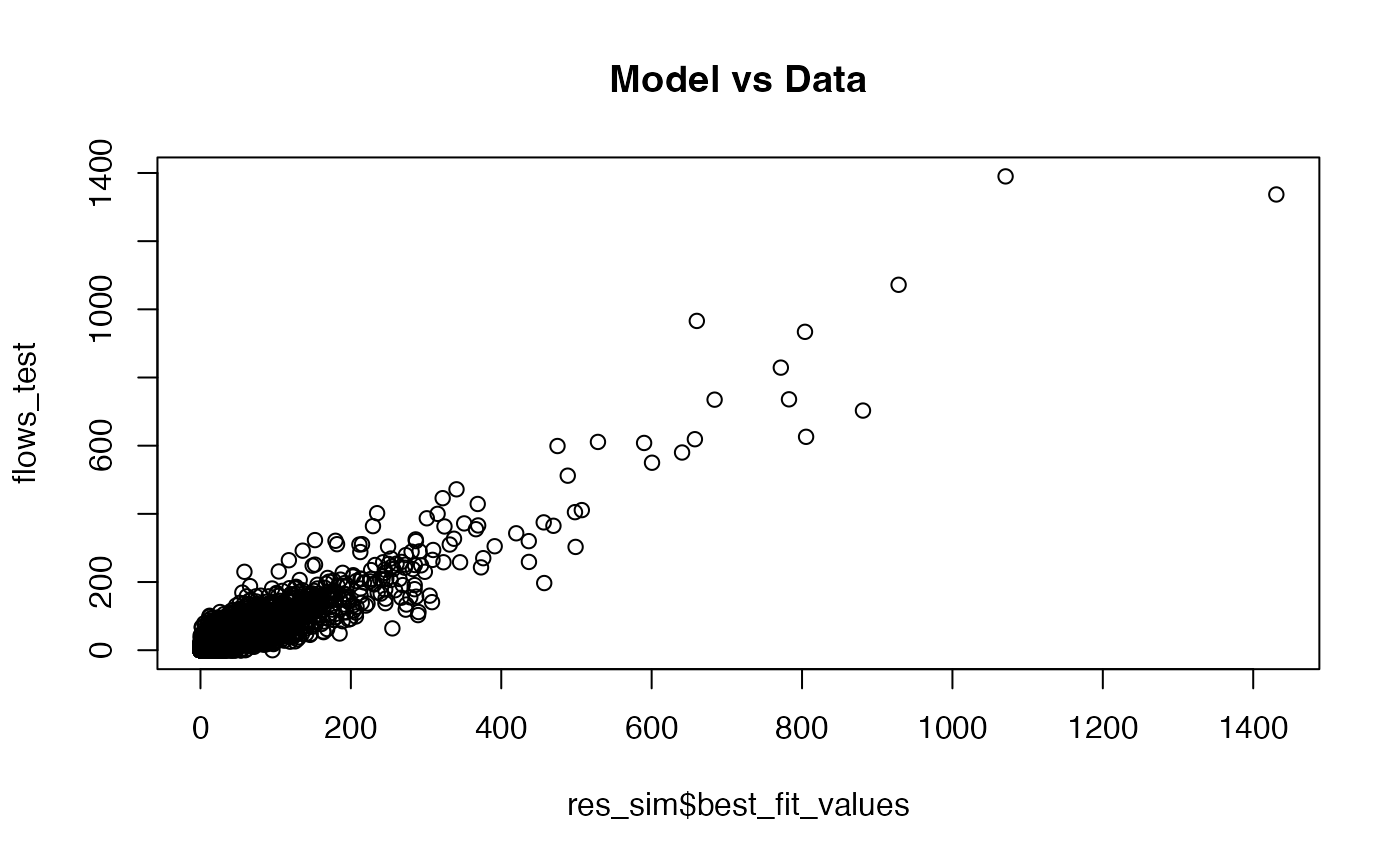
Let’s see how the model output correlates with the observed data:

cor(x=c(res_sim$best_fit_values)
    ,y=c(flows_test))
#> [1] 0.9287456